오늘은 머신러닝 기법 중 하나인 Decision Tree에 대해서 포스팅해보도록 하겠습니다.
참고한 책은 Hands On Machine Learning 입니다.
Decision Tree는 의사 결정 나무라고도 하는데, classification과 regression, 심지어 multi-output task에까지 사용될 수 있는 머신러닝 알고리즘입니다.
Decision Tree는 유명한 머신러닝 기법인 Random Forests에서 사용되는 요소이기도 합니다.
(Random Forests는 다음에 포스팅하는걸로..)
1. Making Predictions

Decision Tree는 어떤 식으로 예측을 진행할까요?
쉽게 이해하기 위해, 붓꽃(Iris)을 분류하는 태스크를 생각해보겠습니다.
가장 먼저 맨 꼭대기인 root node부터 시작합니다. (depth 0)
root node의 기준에 따라서, 만약에 꽃잎의 길이가 2.45cm보다 작거나 같다면 왼쪽의 노드로, 크다면 오른쪽 아래의 노드로 내려갑니다.
이렇게 root node에 달려있는 노드들을 자식 노드, child node라고 합니다.
또한 왼쪽 노드처럼 더이상 자식 노드가 없는 노드를 잎 노드 (단말 노드), leaf node라고 합니다.
2.45cm보다 짧아 왼쪽 자식노드로 내려간 데이터들은 'setosa' 클래스로 분류되었습니다.
그렇다면 오른쪽의 노드로 내려간 노드들은 어떻게 진행될까요?
오른쪽 노드는 자식 노드를 갖고 있으니, 노드의 기준에 따라 또 클래스가 분류됩니다.
꽃잎의 넓이가 1.75cm보다 작다면 왼쪽 노드로 내려가 versicolor로,
크다면 오른쪽 자식 노드로 내려가 virginica로 분류됩니다.
Decision Tree의 장점은 매우 적은 데이터셋으로도 학습이 가능하며, 데이터셋을 scaling하거나 centering해줄 필요가 없다는 점입니다.
대충 여러 개의 노드 내에서 기준을 삼고 그에 따라 클래스가 분류되는 형태로 보입니다.
그렇다면 위의 그림에 노드들에 있는 gini, samples 등의 attribute는 무엇을 가리킬까요?
Attiributes
samples : 학습 인스턴스의 개수, 즉 데이터셋
value : 노드에서 각 클래스별로 samples이 몇 개씩 있는가 (예측 결과)
gini : impurity
위의 그림에서 대입해보자면 150개의 샘플(붓꽃 데이터셋)로 시작하여 setosa로 50개의 샘플이 분류되었는데,
value를 확인해보면 setosa로 50개가 올바르게 분류된 것을 볼 수 있죠.
나머지 100개는 오른쪽 노드로 내려가 54개는 versicolor로, 46개는 virginica로 분류되었습니다.
그러나 왼쪽 자식 노드의 value를 봤을 때 49개만이 versicolor이고 5개는 virginica인 것을 볼 수 있습니다.
오른쪽 자식 노드를 보면 versicolor가 한 개 잘못 분류된 것을 볼 수 있습니다.
간단하게 설명해보자면 sample은 classification의 결과이며, value는 실제 class라고 볼 수 있습니다.
여기까지는 보통의 분류 태스크와 비슷하여 이해가 쉬운데, gini impurity는 조금 생소합니다. (저만 그럴수도)
Gini impurity
impurity는 한국말로 번역해보자면 '불순물' 정도의 뜻을 갖고 있습니다.
즉, Decision Tree 내에서는 각 노드의 pure의 정도를 나타냅니다.
만약의 어떠한 노드의 gini가 0이라면 그 노드는 모든 샘플이 클래스에 옳게 분류된 것이며, pure하다고 볼 수 있습니다.

위의 수식은 Gini impurity의 수식입니다.
그림 1.을 예시로 하며 depth 2인 왼쪽 노드(versicolor)의 gini를 구해보도록 하겠습니다.
수식 1.에서 p는 i번째 노드에서의 샘플 내에서 클래스 k의 비율입니다.
그림 1.에서 붓꽃의 클래스는 3개이므로 n=3이고, 해당 노드의 샘플 개수는 54개입니다.
value를 봤을 때 샘플 중에서 클래스 setosa는 0개, versicolor는 49개, virginica는 5개이므로 의 gini impurity를 가지고 있습니다.
만약 모든 샘플이 옳게 분류되었다면 샘플의 개수가 49개가 되겠고, 이 되겠네요.
attiribute 설명은 이정도로 마치고 다시 설명을 이어가겠습니다.
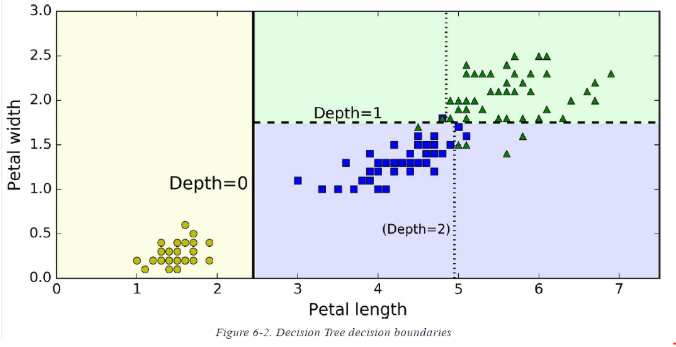
그림 2번은 그림 1번의 Decision Tree의 decision boundaries, 결정 경계입니다.
수직으로 진하게 그려진 선이 root node를 구분하는 decision boundary로, 꽃잎의 길이가 2.45cm 이하인 setosa 클래스입니다.
이 부분은 gini impurity가 0으로 모두 setosa이기 때문에 더 이상 분류할 수 없습니다.
그렇다면 오른쪽으로 넘어갑니다.
오른쪽은 impure하기 때문에 분류를 더 진행합니다.
왼쪽 축인 꽃잎의 넓이를 기준으로 하여 1.75cm 이하는 versicolor로, 이상은 virginica로 분류되었습니다.
그러나 분류 결과가 완벽하지 않은 것을 볼 수 있는데, 책을 보시면 아시겠지만 이 Decision Tree의 maximum depth는 2로 설정되어있기 때문입니다.
만약 3으로 설정되어있다면 수직 점선 또한 새로운 boundary가 될 수 있겠네요.
White Box vs Black Box
이렇게 보다시피 Decision Tree는 매우 직관적이고 예측 결과를 해석할 수 있습니다.
이러한 모델들을 white box 모델이라고 부릅니다.
반대로, 이후에 포스팅할 Random Forests나 딥러닝의 neural network의 경우는 balck box model이라고 부릅니다.
예측에 있어서 좋은 성능을 보이고, 내부에서의 연산 과정을 확인할 수는 있으나
예측 결과에 대한 근거를 설명할 수 없기 때문이라고 합니다.
얘를 들어서, 만약에 neural network가 사진에 특정한 인물이 있다고 예측(segementation, detection)한다면 어떠한 요소가 network의 prediction에 도움을 준 것일까요?
인물의 눈인지, 코, 입인지, 신발인지, 그 인물이 앉은 의자인지.. 인간의 입장에서 알 수 없습니다.
따라서 Decision Tree는 이런 부분에 있어서 간단한 분류 rule을 제공하며 직관적이라는 장점이 있습니다.
2. Estimating Class Probabilites
Decision Tree는 인스턴스가 특정한 클래스 k에 속할 probability를 측정할 수 있습니다.
분류만 하는 것이 아니라, 해당 클래스로 분류가 될 확률도 추정하는 것입니다.

인스턴스 중 하나가 꽃잎의 길이가 5cm이고 넓이가 1.5cm라고 합시다.
그렇다면 그림 1번의 Decision Tree에서, 이 인스턴스는 depth 2인 왼쪽 자식 노드로 내려가야하는데,
이 노드의 경우 각 클래스별로 Setosa : 0/54 (0%), Versicolor : 49/54 (90.7%), Virginica : 5/54 (9.3%) 의 확률로 분류해야합니다.
따라서 클래스 분류를 할 경우 Versicolor의 확률이 가장 높기 때문이 본 클래스로 분류될 것입니다.
이렇게 Decision Tree의 전반적인 내용을 살펴봤습니다.
저는 Python을 사용해서 scikit-learn에서 제공하는 패키지를 사용합니다.
밑에는 iris dataset을 이용하여 분류하고, 해당 인스턴스가 각 클래스에 대해 얼만큼의 probability를 가지는지를 보여주는 코드입니다.
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data[:, 2:] # petal length and width
y = iris.target
tree_clf = DecisionTreeClassifier(max_depth=2)
tree_clf.fit(X, y)
# Result
>> DecisionTreeClassifier(class_weight=None, criterion='gini', max_depth=2,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, presort=False,
random_state=None, splitter='best')
tree_clf.predict_proba([[5, 1.5]])
# Result
>> array([[0. , 0.90740741, 0.09259259]])
tree_clf.predict([[5, 1.5]])
# Result
>> array([1]) #Versicolor
다음 포스팅에선 scikit-learn에서 제공하는 CART 알고리즘에 대해서 이어서 설명하도록 하겠습니다.
틀린 부분 있으면 댓글로 남겨주세요. 감사합니다.
'ML | DL' 카테고리의 다른 글
| [Review] Automated detection of third molars and mandibular nerve by deep learning (0) | 2020.12.18 |
|---|---|
| [Review] LS-Net : Fast Single-Shot Line-Segment Detector (0) | 2020.07.29 |
| [Keras] fit vs fit_generator (0) | 2020.07.15 |
| [Keras] Sequential vs Functional (0) | 2020.07.15 |
| [DL] Activation Function (활성화 함수) (0) | 2020.07.14 |



